Rubinstein Bargaining!

Rubinstein Bargaining:

Single negotiation:  offer and counteroffers

Bad Idea:

Offer/ Counteroffer

It’s better to strike a deal Sooner than later

A deal today > same deal tomorrow

$1 > $1

A deal could make a deal smaller

The Risk:  Loyal customers develop relationships with other shipping agents.  NHL collective baragaining games can never be replayed

Shrinks pie by half each day.

100 -> 50 -> 25 -> 12.5 ->....

Bea should never accept zero:  Bea can guarantee herself far more than zero.

100-> 25/25 (if abe turns down the offer)  the pie will shrink to 25

Abe couldn’t get more than 25, b/c that’s how much is going around

Key point:  25 on Tuesday Bea can get 25 for herself on Tuesday, no reason to get 25 on Monday.

Bea should never accept anything less than <=(Tomorrow’s pie - the day after tomorrow’s pie)

50- 25 = 25

25 -> 12.5(Thursday) -> 6.25 (friday)-> 3.125(sat) -> 1.5621 (sun)

Bea shouldn’t take less than 25% of the 25 or 6.25  (25* .25) = 6.25

Bea could counter offer on Thursday with an offer of 6.25  ( 3.125 - 1.5621) =

Abe must concede at least 25% or 6.25 to get Bea to agree

Abe’s Wednesday value is 75% of 25 or 18.75  (.75 * 25) = 18.75

Abe only has to counter with 18.75 on Tuesday.

Bea gets to keep 31.25 on Tuesday.

Abe gets to keep

Where this all ends up:

Time-consistent lower bound for BEA % ; the least Bea will accept in the future; the least BEA should accept today

Bea’s Lowest Bound:  L >=25%  must show L >= 31.25%  L=?

What is the least Bea could get if she turns down Monday’s offer?

Wednesday Abe has to at least offer her

That’s the best abe can do on Wednesday

Bea will hold out for atleast L share in the future.   

.5 - .25(1*L) of 1 or 50 -25(1-L) of 100

Thus Bea’s min percentage will be consistent over time if and only if:  L = .50 - .25 (1 - L)

L= ⅓ or 33.3%

If Bea can never take less than (25 * 33.3%) of the pie the most Abe can get is 25 *(⅔) of the pie

If Bea offer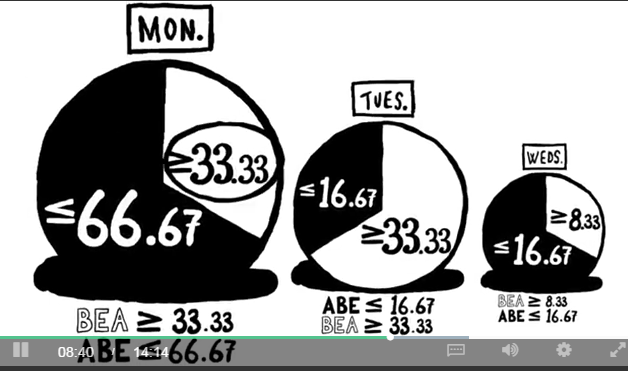

What is the most BEA could get?  M = ⅓

Abe poitns out the most she gets on Tuesday si 50, 50 is the very best she could do on Monday.

Bea <= 12.5, Abe >= 12.5

Time consistent upper bound for Bea, the most Bea could ever get is 33.3% of the pie

If she always says yes on Thursday then

Accept any offer reject any offer below a 30% and accept any offer above 30% of the pie.

Proposer gets ⅔ of the pie and receiver gets ⅓ of the pie.

Monday Abe offers ⅓ of the pie

Tuesday Bea offers ⅓ of the pie

How much more the proposer gets vs the receiver gets depends on how fast the pie shrinks 1% per day then the inbalance gets much smaller…  proposer gets 100/199 or 50.25%

Receiver gets 99/199 of 49.75%

The power in the game is limited to on’es ability to cause a day’s worth of delay.

Abe gets 50% + (33.3% * 50%) = 2/3

Sigma = 50% ; proposer gets ⅔ receiver gets ⅓

As the shrinkage rates get lower and lower, the ability to move first becomes less important, the solution to the game converges to 50%/50%

If the pie shrinks from 1 to delta each day:

1/(1+ delta) for the proposer

delta/(1+delta) for the receiver

Delta = ½

⅔ for the proposer

Delta  = 99%

1/1.99 for the proposer

50.25 for the proposer 1/1.990  

As the pie shrinks less between rounds, there’s less of an advantage from going first and so the division gets closer to 50, 50.  

If offers and counter offers is in hours

What matters is the shrinkage, not the time.

Offers made with little loss inbetween them then it can be 50/50.